Google CTF 2022 - Eldar Writeup
Last weekend, I particpated in Google CTF with my team idek. I manage to solve one challenge and our team placed 20th. This is a write for eldar (333pt/14 solves) a rev challenge.
Preamble⌗
This challenge took me >24 hours and it is my first hard solve ever in Google CTF. My approach to this challenge is certainly not clever and I implore you to check out the great writeups from lkmidas and hgarrereyn
To recap this challenge, the binary is found to contain a flag checker program in the elf relocations. Using a random paper from 2013, ld source code and plain reversing, we can find small snippings of self-modifying code and shellcode.
Initial Findings⌗
Challenge files can be found here.
We found this app on a recent Ubuntu system, but the serial is missing from
serial.c. Can you figure out a valid serial?Just put it into
serial.cand run the app withmake && make run.Thanks!
Note: you don’t have to put anything else other than the serial into
serial.cto solve the challenge.
What we see is a very simple Makefile and serial.c
// Copyright 2022 Google LLC
//
// Licensed under the Apache License, Version 2.0 (the "License");
// you may not use this file except in compliance with the License.
// You may obtain a copy of the License at
//
// https://www.apache.org/licenses/LICENSE-2.0
//
// Unless required by applicable law or agreed to in writing, software
// distributed under the License is distributed on an "AS IS" BASIS,
// WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
// See the License for the specific language governing permissions and
// limitations under the License.
char serial[] = "";
# Copyright 2022 Google LLC
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
# You may obtain a copy of the License at
#
# https://www.apache.org/licenses/LICENSE-2.0
#
# Unless required by applicable law or agreed to in writing, software
# distributed under the License is distributed on an "AS IS" BASIS,
# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
# See the License for the specific language governing permissions and
# limitations under the License.
serial:
gcc -shared -o libserial.so serial.c
run:
./eldar
clean:
rm libserial.so > /dev/null
Running eldar tells us if the flag is valid or not
joshual@fedora:eldar$ make
gcc -shared -o libserial.so serial.c
joshual@fedora:eldar$ make run
./eldar
Sorry, but this serial number is not valid!Ok, opening it up in binary ninja, we see nothing?
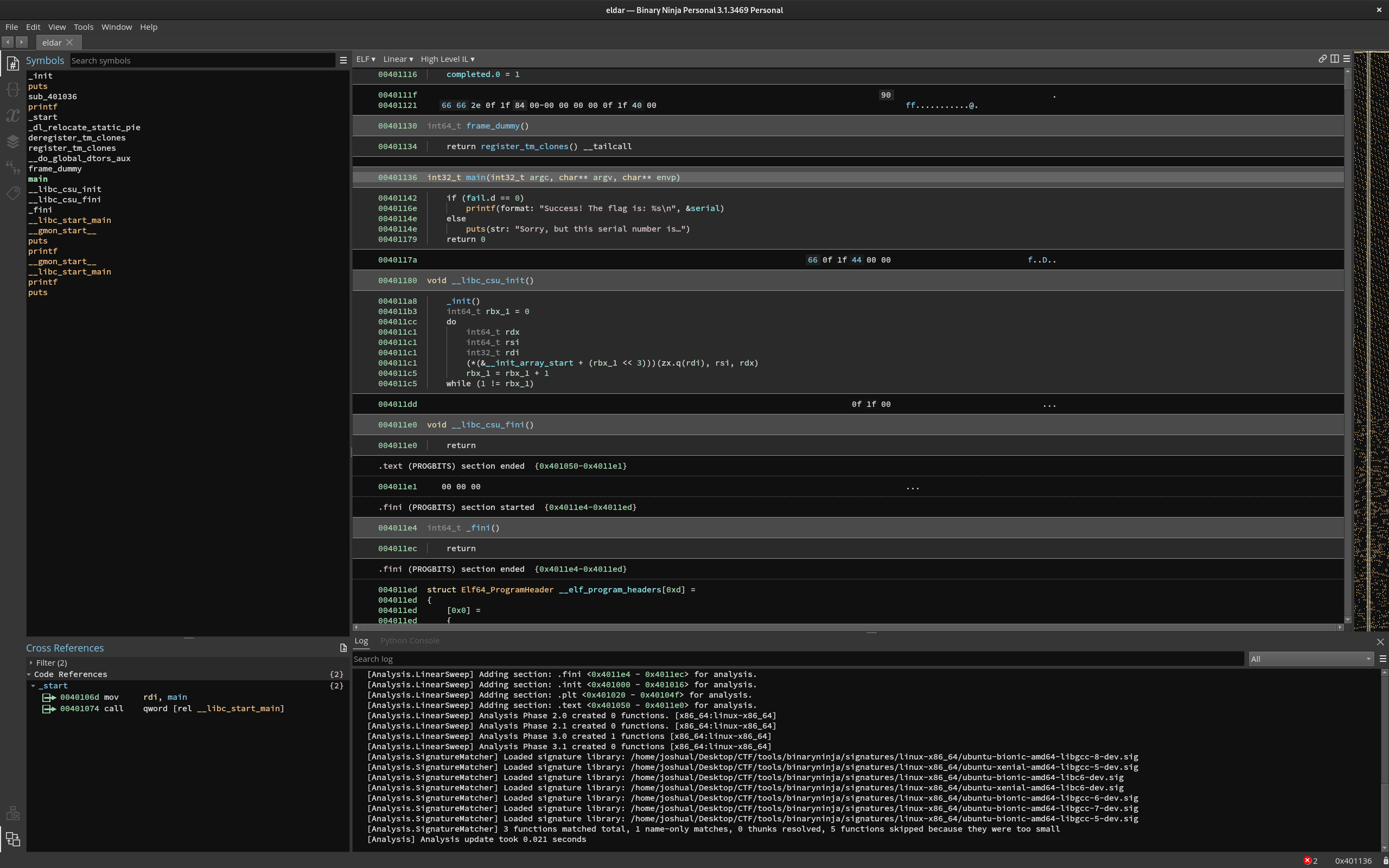
I thought the core logic was perhaps hidden in the _init function or something but nothing fruitful. I also noticed a very large section of data on the side and assumed that has to be the core logic. But how do we understand this logic? Well, one of my teammates were using ida and found a lead
Hm, as we can see, seems like this challenge has to do something related to the elf metadata, specifically relocations. We can list the relocations with readelf -r eldar
joshual@fedora:eldar$ readelf -r eldar > readelf.txt
joshual@fedora:eldar$ head readelf.txt
Relocation section '.rela.dyn' at offset 0x4272 contains 102003 entries:
Offset Info Type Sym. Value Sym. Name + Addend
000000403ff0 000d00000006 R_X86_64_GLOB_DAT 0000000000000000 __libc_start_main@GLIBC_2.2.5 + 0
000000403ff8 000e00000006 R_X86_64_GLOB_DAT 0000000000000000 __gmon_start__ + 0
000000404040 000f00000005 R_X86_64_COPY 0000000000404040 serial + 0
000000804000 000000000008 R_X86_64_RELATIVE 0
000000804000 000000000008 R_X86_64_RELATIVE 0
000000804000 000000000008 R_X86_64_RELATIVE 0
000000804000 000000000008 R_X86_64_RELATIVE 0
joshual@fedora:eldar$ wc -l readelf.txt
102011 readelf.txtWhy are there 100k lines of elf relocations? This must be our flag checker. Let’s investigate!
“Weird Machines” in ELF⌗
Looking at a random part of the elf relocations, we see the following.
0000008040a4 000000000008 R_X86_64_RELATIVE 8
000000928c92 000200000005 R_X86_64_COPY 0000000000804000 ^B + 0
0000008040cc 000400000001 R_X86_64_64 0000000000804000 ^D + 0
000000928c92 000000000008 R_X86_64_RELATIVE 0
0000008040cd 00010000000a R_X86_64_32 0000000000000000 ^A + 0
00000080409c 000000000008 R_X86_64_RELATIVE 8043fa
0000008040fc 000200000005 R_X86_64_COPY 0000000000804000 ^B + 0
00000080409c 000000000008 R_X86_64_RELATIVE 8040cc
000000928d3a 000200000005 R_X86_64_COPY 0000000000804000 ^B + 0
0000008040e4 000400000001 R_X86_64_64 0000000000804000 ^D + 0So what are R_X86_64_RELATIVE, R_X86_64_COPY, R_X86_64_64, and R_X86_64_32? After a bit of searching, I found some relevant source code and a paper titled ‘“Weird Machines” in ELF: A Spotlight on the Underappreciated Metadata’.
First, the paper explained that it is possible to use the instructions above to create a turing complete language. More importantly, it showed how each instruction are equivalent to
| Type | Instruction |
|---|---|
| Relo(type=R_X86_64_RELATIVE, offset=0xbeef0000, symbol=0, addend=0x04) | mov [0xbeef0000], 0x04 |
| Relo(type=R_X86_64_COPY, offset=0xbeef0000, symbol=var, addend=0x04) | mov [0xbeef0000], [var] |
| Relo(type=R_X86_64_64, offset=0xbeef0000, symbol=var, addend=0x04) | add [0xbeef0000], var, 0x04 |
Note: add X, Y, Z translate to X = Y + Z
The paper also talks about jumping but we ignored it as there are already a huge amount of relocations and assumed there would not be any jumping. Knowing this, we wrote up our (first) script
f = open('dump.txt','r').read().split('\n')[1:]
OFFSET_MAPPINGS = {
0x8042ba: "\\x00",
0x8042c2: "\\x01",
...
0x804ab2: "\\xff",
0x804084: 'A',
0x80409c: 'B',
0x8040b4: 'C',
0x8040cc: 'D',
0x8040e4: 'E',
0x8040fc: 'F',
0x804114: 'G',
0x80412c: 'H',
0x804144: 'I',
0x80415c: 'J',
0x404060: 'fail',
}
class Relo:
def __init__(self, line):
self.line = line
self.offset = self.parse_offset(int(line[:14].strip(),16))
self.info = int(line[14:27].strip(),16)
self.type = line[27:45].strip()
self.value = line[45:62].strip()
self.name = self.parse_name(line[62:].strip())
def parse_offset(self, offset):
if offset in OFFSET_MAPPINGS:
return OFFSET_MAPPINGS[offset]
return '[{}]'.format(hex(offset))
def parse_name(self, name):
if name == '^B + 0':
return 'B'
if name == '^A + 0':
return 'A'
if name == '^C + 0':
return 'C'
if name == '^D + 0':
return 'D'
if name == '^E + 0':
return 'E'
if name == '^F + 0':
return 'F'
if name == '^G + 0':
return 'G'
name = name.replace('^','')
if '+' in name:
return name
return hex(int(name, 16))
def __str__(self):
return self.line
def relative(relo):
print('mov {}, {}'.format(relo.offset, relo.name))
def copy(relo):
print('mov {}, {}'.format(relo.offset, relo.name))
def sym(relo):
print('add {}, {}'.format(relo.offset, relo.name))
# def sym32(relo):
# pass
opcodes = {
'R_X86_64_RELATIVE': relative,
'R_X86_64_COPY': copy,
'R_X86_64_64': sym,
'R_X86_64_32': sym,
}
instrs = []
for i in f:
instrs.append(Relo(i))
for instr in instrs:
if instr.type in opcodes:
opcodes[instr.type](instr)
else:
print(instr)
Here is the code dump
add [E], E
mov [0x806562], 0
add [E], E + 8042ba
mov [0x8042ba], [E]
mov [0x8065ca], [B]
add [0x0], F
mov [B], 8042c2
mov [0x806622], B
add [D], D
mov [0x806622], 0Ok, that looks better. Wait! what is add [0x0], F? and what are the addressed the relocations are modifying?
This is time sink #1. We spent quite a bit of time wondering what
add [0x0], Fdoes. We originally thought we parsed it wrong and perhaps the address where the value would be stored at is the base address, or a symbols address.
After some time, we also noticed
mov B.st_size, 0x8
mov [0x806352], [B]
add D, D
mov [0x806352], 0x0Why are there two instructions moving to the same address? Wouldn’t that make the first mov instruction obsolete? Looking at 0x806352 in ida, we see it points to addend of
Relo(type=R_X86_64_64, offset=0x8040cc, sym=0x4, addend=0) which is equivalent to add D, D. Here, we see mov [0x806352], [B] will modify the addend of the next instruction and then execute the next instruction.
The code is modifying itself! We need a more complex disassembler.
Emulating Relocations⌗
What we did to write a better disassembler is to emulate the relocation instructions and disassemble.
R_X86_64_RELATIVE is pretty straight forward
def relative(r_offset, r_symbol, r_addend):
print('mov {}, {}'.format(parse_addr(r_offset), parse_imm(r_addend)))
elf.write(r_offset, p64(r_addend))But with R_X86_64_COPY, R_X86_64_64, and R_X86_64_32, these all require resolving symbols. How do we go about that?
Knowing elf_machine_rela is the function which performs the relocations, we see sym is passed to the function as an arguement. Looking for references, we see a call to elf_machine_rela in do-rel.h
elf_machine_rel (map, scope, r2,
&symtab[ELFW(R_SYM) (r2->r_info)],
&map->l_versions[ndx],
(void *) (l_addr + r2->r_offset),
skip_ifunc);
Here, sym is passed as &symtab[ELFW(R_SYM) (r2->r_info)] which means the symbol used is the ith index of the symbol table.
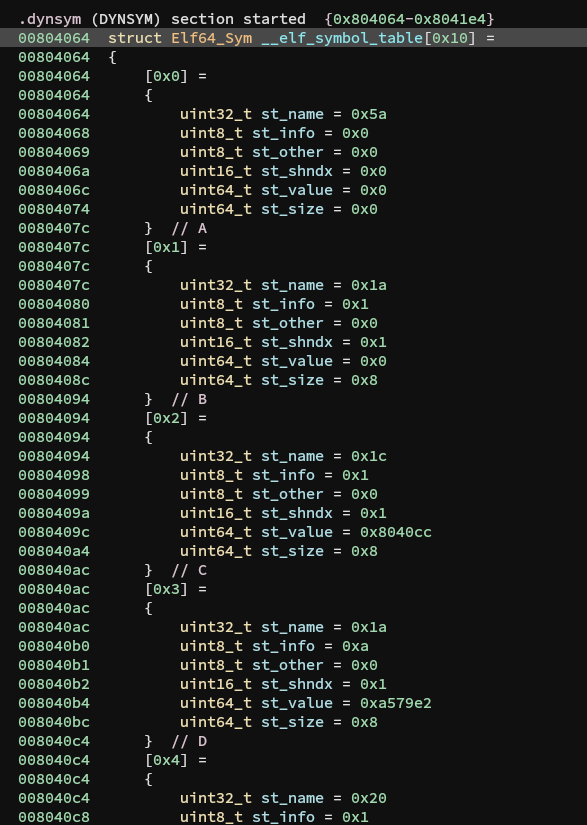
Here, we assign some arbritrary variables to each symbol and create the following mapping
symbols_to_addr = {
1: 0x00804084,
2: 0x0080409c,
3: 0x008040b4,
4: 0x008040cc,
5: 0x008040e4,
6: 0x008040fc,
7: 0x00804114,
8: 0x0080412c,
9: 0x00804144,
10: 0x0080415c,
}
symbols_lookup = {
1: 'A',
2: 'B',
3: 'C',
4: 'D',
5: 'E',
6: 'F',
7: 'G',
8: 'H',
9: 'I',
10: 'J',
}Knowing this, we can emulate the remaining instructions
def copy(r_offset, r_symbol, r_addend):
if r_symbol not in symbols_lookup:
print("AAAAAA", hex(r_symbol))
exit(0)
sz = u64(elf.read(symbols_to_addr[r_symbol]+8, 8))
print('mov {}, [{}] ({} bytes)'.format(parse_addr(r_offset), symbols_lookup[r_symbol], sz))
data = u64(elf.read(symbols_to_addr[r_symbol], 8))
data = elf.read(data, sz)
elf.write(r_offset, data)
def sym(r_offset, r_symbol, r_addend):
if r_symbol not in symbols_lookup:
print("AAAAAA", hex(r_symbol))
exit(0)
if r_addend == 0:
print('add64 {}, {}'.format(parse_addr(r_offset), symbols_lookup[r_symbol]))
else:
print('add64 {}, {} + {}'.format(parse_addr(r_offset), symbols_lookup[r_symbol], hex(r_addend)))
st_info = u8(elf.read(symbols_to_addr[r_symbol]-4, 1))
sym_val = u64(elf.read(symbols_to_addr[r_symbol], 8))
elf.write(r_offset, p64((r_addend+sym_val)&0xffffffffffffffff))
def sym32(r_offset, r_symbol, r_addend):
if r_symbol not in symbols_lookup:
print("AAAAAA", hex(r_symbol))
exit(0)
if r_addend == 0:
print('add32 {}, {}'.format(parse_addr(r_offset), symbols_lookup[r_symbol]))
else:
print('add32 {}, {} + {}'.format(parse_addr(r_offset), symbols_lookup[r_symbol], hex(r_addend)))
sym_val = u64(elf.read(symbols_to_addr[r_symbol], 8))
elf.write(r_offset, p32((r_addend+sym_val)&0xffffffff))Putting this all together, we have
from pwn import *
import re
context.log_level = 'error'
context.arch = 'amd64'
OFFSET_MAPPINGS = {
0x8042ba: "var_00",
0x8042c2: "var_01",
0x8042ca: "var_02",
0x8042d2: "var_03",
...
0x804ab2: "var_ff",
0x804084: 'A',
0x80409c: 'B',
0x8040b4: 'C',
0x8040cc: 'D',
0x8040e4: 'E',
0x8040fc: 'F',
0x804114: 'G',
0x80412c: 'H',
0x804144: 'I',
0x80415c: 'J',
0x404060: 'fail',
}
symbols_lookup = {
1: 'A',
2: 'B',
3: 'C',
4: 'D',
5: 'E',
6: 'F',
7: 'G',
8: 'H',
9: 'I',
10: 'J',
}
symbols_to_addr = {
1: 0x00804084,
2: 0x0080409c,
3: 0x008040b4,
4: 0x008040cc,
5: 0x008040e4,
6: 0x008040fc,
7: 0x00804114,
8: 0x0080412c,
9: 0x00804144,
10: 0x0080415c,
}
elf = ELF('eldar')
def parse_addr(addr):
if addr in OFFSET_MAPPINGS:
return OFFSET_MAPPINGS[addr]
return '[{}]'.format(hex(addr))
def parse_imm(imm):
if imm in OFFSET_MAPPINGS:
return '&'+OFFSET_MAPPINGS[imm]
return hex(imm)
def relative(r_offset, r_symbol, r_addend):
print('mov {}, {}'.format(parse_addr(r_offset), parse_imm(r_addend)))
elf.write(r_offset, p64(r_addend))
def copy(r_offset, r_symbol, r_addend):
if r_symbol not in symbols_lookup:
print("AAAAAA", hex(r_symbol))
exit(0)
sz = u64(elf.read(symbols_to_addr[r_symbol]+8, 8))
print('mov {}, [{}] ({} bytes)'.format(parse_addr(r_offset), symbols_lookup[r_symbol], sz))
data = u64(elf.read(symbols_to_addr[r_symbol], 8))
data = elf.read(data, sz)
elf.write(r_offset, data)
def sym(r_offset, r_symbol, r_addend):
if r_symbol not in symbols_lookup:
print("AAAAAA", hex(r_symbol))
exit(0)
if r_addend == 0:
print('add64 {}, {}'.format(parse_addr(r_offset), symbols_lookup[r_symbol]))
else:
print('add64 {}, {} + {}'.format(parse_addr(r_offset), symbols_lookup[r_symbol], hex(r_addend)))
st_info = u8(elf.read(symbols_to_addr[r_symbol]-4, 1))
sym_val = u64(elf.read(symbols_to_addr[r_symbol], 8))
elf.write(r_offset, p64((r_addend+sym_val)&0xffffffffffffffff))
def sym32(r_offset, r_symbol, r_addend):
if r_symbol not in symbols_lookup:
print("AAAAAA", hex(r_symbol))
exit(0)
if r_addend == 0:
print('add32 {}, {}'.format(parse_addr(r_offset), symbols_lookup[r_symbol]))
else:
print('add32 {}, {} + {}'.format(parse_addr(r_offset), symbols_lookup[r_symbol], hex(r_addend)))
sym_val = u64(elf.read(symbols_to_addr[r_symbol], 8))
elf.write(r_offset, p32((r_addend+sym_val)&0xffffffff))
opcodes = {
8: relative,
5: copy,
1: sym,
10: sym32,
}
sym_table = 0x00804064
elf_relo = 0x00804ab2
for _ in range(102000):
r_offset = u64(elf.read(elf_relo, 8))
type = u32(elf.read(elf_relo+8, 4))
r_symbol = u32(elf.read(elf_relo+12, 4))
r_addend = u64(elf.read(elf_relo+16, 8))
regs = []
for i in range(1, 11):
regs.append(u64(elf.read(symbols_to_addr[i], 8)))
args = list(map(hex, regs))
if type in opcodes:
opcodes[type](r_offset, r_symbol, r_addend)
else:
print("AAAAA", hex(type))
exit(0)
elf_relo += 24
mov [0x811cf2], 0x0
mov B, 0x404040
mov B.st_size, 0x1
mov G, [B] (1 bytes)
mov B, &G
mov B.st_size, 0x8
mov [0x811db2], [B] (8 bytes)
add64 D, D + 0x804000
mov [0x811db2], 0x0
add32 [0x8040cd], AThat looks better, so we began to reverse the instructions.
mov var_00, 0x0
mov var_01, 0x1
mov var_02, 0x2
...
mov var_fc, 0xfc
mov var_fd, 0xfd
mov var_fe, 0xfe
mov var_ff, 0xff
mov D, 0x0
mov B, &var_00
mov [0x8040a4], 0x8
mov [0x806352], [B] (8 bytes)
add64 D, D
mov [0x806352], 0x0
mov B, 0x404040
mov [0x8040a4], 0x1
mov G, [B] (1 bytes)
mov B, &G
mov [0x8040a4], 0x8
mov [0x806412], [B] (8 bytes)
add64 D, D + 0x804000
mov [0x806412], 0x0
Ok, so looking at the beginning of the instructions, we see several the program reading and writing to 0x404040, 0x8040a4 and 0x806352
As we have found before, the pattern
mov [0x806352], [B] (8 bytes)
add64 D, D
mov [0x806352], 0x0
modifies the add64 instruction. In this case, 0x806352 is the address of addend in add64. 0x8040a4 is the address on the symbol table, specifically B.st_size.
0x404040 is the address of serial, our input.
We can update OFFSET_MAPPINGS to include 0x8040a4 and 0x404040
mov D, 0x0
mov B, &var_00
mov B.st_size, 0x8
mov [0x806352], [B] (8 bytes)
add64 D, D
mov [0x806352], 0x0
mov B, &serial
mov B.st_size, 0x1
mov G, [B] (1 bytes)
mov B, &G
mov B.st_size, 0x8
mov [0x806412], [B] (8 bytes)
add64 D, D + 0x804000
mov [0x806412], 0x0
Looking at mov B, &serial and onwards, we see if moves the first byte of serial into G, and moves the value of G into 0x806412. Thus if serial="ABC" then the instructions above should look like
mov [0x806412], [B] (8 bytes)
add64 D, D + 0x41
mov [0x806412], 0x0
We can set the flag with
elf.write(0x404040, "ABC")
Try running it now,
joshual@fedora:eldar$ python disas.py
Traceback (most recent call last):
File "disas.py", line 363, in <module>
elf.write(0x404040, "ABC")
File "/home/joshual/.local/lib/python2.7/site-packages/pwnlib/elf/elf.py", line 1444, in write
offset = self.vaddr_to_offset(address)
File "/home/joshual/.local/lib/python2.7/site-packages/pwnlib/elf/elf.py", line 1304, in vaddr_to_offset
offset = address - segment.header.p_vaddr
AttributeError: 'str' object has no attribute 'header'
Huh, seems like pwntools is not able to resolve the address of serial. So we instead hardcode the values in the emulator.
Note the same error pops up when writing to
failso that value is hardcoded as well
def relative(r_offset, r_symbol, r_addend):
print('mov {}, {}'.format(parse_addr(r_offset), parse_imm(r_addend)))
if r_offset != 0x404060: # fail variable
elf.write(r_offset, p64(r_addend))
def copy(r_offset, r_symbol, r_addend):
if r_symbol not in symbols_lookup:
print("AAAAAA", hex(r_symbol))
exit(0)
sz = u64(elf.read(symbols_to_addr[r_symbol]+8, 8))
print('mov {}, [{}] ({} bytes)'.format(parse_addr(r_offset), symbols_lookup[r_symbol], sz))
if r_offset != 0x404060: # fail variable
data = u64(elf.read(symbols_to_addr[r_symbol], 8))
if 0x404040 <= data <= 0x404040+32:
data -= 0x404040
data = flag[data:data+sz]
else:
data = elf.read(data, sz)
elf.write(r_offset, data)
def sym(r_offset, r_symbol, r_addend):
if r_symbol not in symbols_lookup:
print("AAAAAA", hex(r_symbol))
exit(0)
if r_addend == 0:
print('add64 {}, {}'.format(parse_addr(r_offset), symbols_lookup[r_symbol]))
else:
print('add64 {}, {} + {}'.format(parse_addr(r_offset), symbols_lookup[r_symbol], hex(r_addend)))
st_info = u8(elf.read(symbols_to_addr[r_symbol]-4, 1))
sym_val = u64(elf.read(symbols_to_addr[r_symbol], 8))
elf.write(r_offset, p64((r_addend+sym_val)&0xffffffffffffffff))
def sym32(r_offset, r_symbol, r_addend):
if r_symbol not in symbols_lookup:
print("AAAAAA", hex(r_symbol))
exit(0)
if r_addend == 0:
print('add32 {}, {}'.format(parse_addr(r_offset), symbols_lookup[r_symbol]))
else:
print('add32 {}, {} + {}'.format(parse_addr(r_offset), symbols_lookup[r_symbol], hex(r_addend)))
sym_val = u64(elf.read(symbols_to_addr[r_symbol], 8))
elf.write(r_offset, p32((r_addend+sym_val)&0xffffffff))
Ok, we can see the 0x41 in the add64!
mov D, 0x0
mov B, &var_00
mov B.st_size, 0x8
mov [0x806352], [B] (8 bytes)
add64 D, D
mov [0x806352], 0x0
mov B, 0x404040
mov B.st_size, 0x1
mov G, [B] (1 bytes)
mov B, &G
mov B.st_size, 0x8
mov [0x806412], [B] (8 bytes)
add64 D, D + 0x804041
mov [0x806412], 0x0
Reversing the Flag Part 1⌗
Ok, that we have an accurate enough disassembly, we can begin reversing. The disassembly dump can be found here
Some notes:
- we represent the
var_XXasmem[XX]
mov D, 0x0
# D = 0
mov B, &var_00
mov B.st_size, 0x8
mov [0x806352], [B] (8 bytes)
add64 D, D
mov [0x806352], 0x0
# D+=mem[0]
mov B, 0x404040
mov B.st_size, 0x1
mov G, [B] (1 bytes)
mov B, &G
mov B.st_size, 0x8
mov [0x806412], [B] (8 bytes)
add64 D, D + 0x804041
mov [0x806412], 0x0
# D += serial[0]
add32 [0x8040cd], A
# ???
mov B, &var_00
mov F, [B] (8 bytes)
# F = mem[0]
mov B, &D
mov [0x8064ba], [B] (8 bytes)
add64 E, D + 0x41
mov [0x8064ba], 0x0
mov B, &E
mov [0x80651a], [B] (8 bytes)
add64 E, E + 0x82
mov [0x80651a], 0x0
mov [0x806562], [B] (8 bytes)
add64 E, E + 0x104
mov [0x806562], 0x0
add64 E, E + 0x8042ba
# E = D*8+0x8042ba
mov var_00, [E] (8 bytes)
# mem[0] = *E
mov [0x8065ca], [B] (8 bytes)
add64 var_41, F
# mem[mem[0]] = F
mov B, &var_01
mov [0x806622], [B] (8 bytes)
add64 D, D + 0x1
# D += mem[1]
mov [0x806622], 0x0
mov B, 0x404041
mov B.st_size, 0x1
mov G, [B] (1 bytes)
mov B, &G
mov B.st_size, 0x8
mov [0x8066e2], [B] (8 bytes)
add64 D, D + 0x804042
mov [0x8066e2], 0x0
# D += serial[1]
add32 [0x8040cd], A
So there few things we can notice,
- There is a repeating pattern
add32 [0x8040cd], Adoes not make much sense- What is
# E = D*4+0x8042badoing?
First looking at add32 [0x8040cd], A, we notice 0x8040cd is the 7 upper bytes of D.st_value, and as A=0. This is roughly equivalent to D &= 0xff. And for # E = D*8+0x8042ba, 0x8042ba is the address of mem[0] and thus D*8+0x8042ba=&mem[D]
This is time sink #2, we spent most of our time trying to find patterns and disassemble by hand.
This piece of disassembly repeats 256 times, alternating between serial[0] and serial[1]. A python equivalent is
D = 0
mem = list(range(256))
for i in range(256):
D += mem[i]
D += ord(flag[(i&1)+idx])
D %= 256
mem[D],mem[i] = mem[i], mem[D]
After this, we have disassembled the first 7940 lines. Looking at the following, we see
mov D, 0x0
# D = 0
mov B, &var_00
mov [0x83336a], [B] (8 bytes)
add64 D, D + 0x3b
mov [0x83336a], 0x0
# D += mem[0]
add32 [0x8040cd], A
# D &= 0xff
mov F, [B] (8 bytes)
# F = mem[0]
mov B, &D
mov [0x8333fa], [B] (8 bytes)
add64 E, D + 0x3b
mov [0x8333fa], 0x0
mov B, &E
mov [0x83345a], [B] (8 bytes)
add64 E, E + 0x76
mov [0x83345a], 0x0
mov [0x8334a2], [B] (8 bytes)
add64 E, E + 0xec
mov [0x8334a2], 0x0
add64 E, E + 0x8042ba
# E = &mem[D]
mov var_00, [E] (8 bytes)
# mem[0] = mem[D]
mov B, &var_00
mov G, [B] (8 bytes)
# G = mem[0]
mov B, &E
mov [0x833552], [B] (8 bytes)
add64 var_3b, F
# mem[D] = F
mov B, &G
mov [0x8335aa], [B] (8 bytes)
add64 F, F + 0x66
mov [0x8335aa], 0x0
# F += G
add32 [0x8040fd], A
# F &= 0xff
mov B, &F
mov [0x833622], [B] (8 bytes)
add64 E, F + 0xa1
mov [0x833622], 0x0
mov B, &E
mov [0x833682], [B] (8 bytes)
add64 E, E + 0x142
mov [0x833682], 0x0
mov [0x8336ca], [B] (8 bytes)
add64 E, E + 0x284
mov [0x8336ca], 0x0
add64 E, E + 0x8042ba
mov [0x804aca], [E] (8 bytes)
# ?? = mem[F]
# Repeats!
mov B, &var_01
mov [0x83375a], [B] (8 bytes)
add64 D, D + 0x84
mov [0x83375a], 0x0
...
The only unknown part is 0x8040fd which points to some empty memory
The pattern above repeats 3 times and the python equivalent is
D = 0
B = 0
smt = []
for i in range(3):
D += mem[i]
D %= 256
F = mem[i]
mem[i] = mem[D]
G = mem[i]
mem[D] = F
F += G
F %= 256
smt.append(chr(mem[F]))
We have now disassembled the first 64516 lines.
mov B, 0xa5952a
mov B.st_size, 0x810
mov var_00, [B] (2064 bytes)
# Zero out mem
mov D, 0x0
mov E, 0x0
mov G, 0xfffffffffffa00b1
# G = 0xfffffffffffa00b1
mov B, 0x804aca
mov B.st_size, 0x1
mov E, [B] (1 bytes)
# E = smt[0]
mov F, 0x0
mov B, &F
mov B.st_size, 0x8
mov [0x97ec42], [B] (8 bytes)
add64 F, F
mov [0x97ec42], 0x0
mov B, &E
mov [0x97eca2], [B] (8 bytes)
add64 F, F + 0x55
mov [0x97eca2], 0x0
mov B, &F
mov [0x97ed02], [B] (8 bytes)
add64 F, F + 0x55
mov [0x97ed02], 0x0
mov [0x97ed4a], [B] (8 bytes)
add64 F, F + 0xaa
mov [0x97ed4a], 0x0
mov [0x97ed92], [B] (8 bytes)
add64 F, F + 0x154
mov [0x97ed92], 0x0
mov B, &E
mov [0x97edf2], [B] (8 bytes)
add64 F, F + 0x55
mov [0x97edf2], 0x0
mov B, &F
mov [0x97ee52], [B] (8 bytes)
add64 F, F + 0x2fd
mov [0x97ee52], 0x0
mov B, &E
mov [0x97eeb2], [B] (8 bytes)
add64 F, F + 0x55
mov [0x97eeb2], 0x0
mov B, &F
mov [0x97ef12], [B] (8 bytes)
add64 F, F + 0x64f
mov [0x97ef12], 0x0
mov [0x97ef5a], [B] (8 bytes)
add64 F, F + 0xc9e
mov [0x97ef5a], 0x0
mov B, &E
mov [0x97efba], [B] (8 bytes)
add64 F, F + 0x55
mov [0x97efba], 0x0
mov B, &F
mov [0x97f01a], [B] (8 bytes)
add64 F, F + 0x1991
mov [0x97f01a], 0x0
mov B, &E
mov [0x97f07a], [B] (8 bytes)
add64 F, F + 0x55
mov [0x97f07a], 0x0
mov B, &F
mov [0x97f0da], [B] (8 bytes)
add64 G, G + 0x3377
# G += E*155
# Repeats!
mov [0x97f0da], 0x0
mov B, 0x804acb
mov B.st_size, 0x1
mov E, [B] (1 bytes)
Here, we see the code follows the pattern of G += smt[i]*CONST and we have reversed the first 65799 lines.
mov [0x986352], [B] (8 bytes)
add64 G, G + 0x556b
# G += smt
mov [0x986352], 0x0
mov B, 0x8040e7
mov B.st_size, 0x5
mov [0x804117], [B] (5 bytes)
mov B, &G
mov B.st_size, 0x8
mov [0x986412], [B] (8 bytes)
add64 D, D + 0x1069b
mov [0x986412], 0x0
# D += G
# Repeats!
mov G, 0xfffffffffffa608a
mov B, 0x804aca
Finally, we see D+=G. This pattern repeats 41 times.
Using some sublime multiple cursor magic, we extracted the constant multiple and starting G value.
multiplier = [0x3377//0x55,0x95ec//0xca,0xbc80//0xe8,0x781e//0xfa,0x7c8e//0x95,0x3ebc//0x6e,0xb973//0xe1,0xd48//0x28,0x2562//0x6e,0x9217//0x95,0x44a0//0x90,0x1e0//0x8,0xdb69//0xed,0x948//0x58,0x56a//0x16,0x3fe1//0x4f,0xbfd//0x5d,0x1c92//0x35,0x396//0x12,0x459b//0xad,0x2d50//0xc8,0x21bc//0x7f,0x47b8//0x99,0x556b//0xc5,0x5456//0x55,0x1092//0xca,0x8e48//0xe8,0xc738//0xfa,0x2098//0x95,0x3994//0x6e,0x456f//0xe1,0x11f8//0x28,0x3de//0x6e,0x34f7//0x95,0x19e0//0x90,0x60//0x8,0x1f7a//0xed,0xf78//0x58,0x1130//0x16,0x286d//0x4f,0x42d8//0x5d,0x2544//0x35,0x5a//0x12,0x4394//0xad,0x2fa8//0xc8,0x1d45//0x7f,0x1f14//0x99,0xbf9d//0xc5,0x361f//0x55,0x8624//0xca,0x6580//0xe8,0xcd14//0xfa,0x5b61//0x95,0x641e//0x6e,0x2e95//0xe1,0x7f8//0x28,0x64fa//0x6e,0x95//0x95,0x5a00//0x90,0x150//0x8,0xbfa3//0xed,0x4360//0x58,0x5ac//0x16,0x4f0//0x4f,0x3222//0x5d,0x1f78//0x35,0xff6//0x12,0x4bb//0xad,0x6ef0//0xc8,0x301f//0x7f,0x3cf6//0x99,0x11b3//0xc5,0x2981//0x55,0x8e08//0xca,0x89c0//0xe8,0x1964//0xfa,0x76bc//0x95,0x1da6//0x6e,0x384//0xe1,0x12e8//0x28,0x5aaa//0x6e,0x254//0x95,0x46e0//0x90,0x318//0x8,0x8817//0xed,0x48e0//0x58,0x4ba//0x16,0x154b//0x4f,0x179d//0x5d,0x25ae//0x35,0x101a//0x12,0x826d//0xad,0x6590//0xc8,0x329a//0x7f,0x264//0x99,0x7b20//0xc5,0x3872//0x55,0x21ee//0xca,0x9f8//0xe8,0x1482//0xfa,0x9341//0x95,0x24f4//0x6e,0x2a3//0xe1,0xcf8//0x28,0x6040//0x6e,0x425a//0x95,0x5a00//0x90,0x5e8//0x8,0x9420//0xed,0x5178//0x58,0xb2c//0x16,0x232e//0x4f,0x1dca//0x5d,0x1c28//0x35,0x7e//0x12,0x5479//0xad,0x44c0//0xc8,0x5dc3//0x7f,0x5577//0x99,0xa887//0xc5,0x7a3//0x55,0x1484//0xca,0xc020//0xe8,0xe57e//0xfa,0xc39//0x95,0x1054//0x6e,0x5541//0xe1,0x23f0//0x28,0x302//0x6e,0x533b//0x95,0x7080//0x90,0xf8//0x8,0x5d81//0xed,0x1708//0x58,0xce4//0x16,0x5dd//0x4f,0x13fb//0x5d,0x1c5d//0x35,0x546//0x12,0x8e97//0xad,0x1770//0xc8,0x6730//0x7f,0x6cc6//0x99,0x1d3e//0xc5,0x352//0x55,0xab3a//0xca,0xd158//0xe8,0xc256//0xfa,0x8549//0x95,0x6c48//0x6e,0x5eec//0xe1,0x1bd0//0x28,0x5136//0x6e,0x641c//0x95,0x2d00//0x90,0x210//0x8,0x4a1//0xed,0x3a70//0x58,0x9a0//0x16,0x7b7//0x4f,0x52d4//0x5d,0x2d22//0x35,0x97e//0x12,0x9ecf//0xad,0x9920//0xc8,0x7710//0x7f,0x8547//0x99,0x5630//0xc5,0x2b7f//0x55,0x9522//0xca,0xb1a0//0xe8,0x3f7a//0xfa,0x7c8e//0x95,0x4b32//0x6e,0x48f3//0xe1,0x1ce8//0x28,0x2116//0x6e,0x304f//0x95,0x8280//0x90,0x618//0x8,0x465c//0xed,0x1448//0x58,0xa66//0x16,0x2644//0x4f,0x210f//0x5d,0x2df6//0x35,0x56a//0x12,0xa4e4//0xad,0x39d0//0xc8,0x43f7//0x7f,0x6897//0x99,0x4542//0xc5,0x2e7c//0x55,0xb31e//0xca,0x91e8//0xe8,0x5014//0xfa,0x3edc//0x95,0x16c6//0x6e,0xbeb9//0xe1,0x2238//0x28,0x37dc//0x6e,0x4006//0x95,0x65d0//0x90,0x1a0//0x8,0x71df//0xed,0x3180//0x58,0xec8//0x16,0x1c15//0x4f,0x22e//0x5d,0xdaa//0x35,0x11ca//0x12,0x1d0f//0xad,0xb158//0xc8,0x5f4//0x7f,0x7e1b//0x99,0xb288//0xc5,0x406a//0x55,0x22b8//0xca,0x3748//0xe8,0xdac0//0xfa,0x37e//0x95,0xd52//0x6e,0x4f1a//0xe1,0x1ab8//0x28,0x1810//0x6e,0x1589//0x95,0x8d30//0x90,0x408//0x8,0x1638//0xed,0x2e10//0x58,0xbb0//0x16,0x3ea5//0x4f,0x350a//0x5d,0x2293//0x35,0xc84//0x12,0x40e//0xad,0x1450//0xc8,0xf61//0x7f,0x6a62//0x99,0x99e8//0xc5,0x3278//0x55,0x56cc//0xca,0x3da0//0xe8,0x58de//0xfa,0x533b//0x95,0x3ade//0x6e,0x4b96//0xe1,0x1068//0x28,0x51a4//0x6e,0x4543//0x95,0x39f0//0x90,0x608//0x8,0x33d8//0xed,0//0x58, 0x10ee//0x16,0x4dc4//0x4f,0x5d//0x5d,0x31b0//0x35,0x924//0x12,0x2324//0xad,0x44c0//0xc8,0x58cd//0x7f,0x6930//0x99,0x86ab//0xc5,0x381d//0x55,0x1092//0xca,0xb8e0//0xe8,0xf03c//0xfa,0x89f1//0x95,0x497a//0x6e,0xcf6c//0xe1,0x12e8//0x28,0x5b86//0x6e,0xf22//0x95,0x84c0//0x90,0x7b0//0x8,0xd227//0xed,0x2520//0x58,0xbdc//0x16,0x32eb//0x4f,0x2b3b//0x5d,0x173//0x35,0x32a//0x12,0x8474//0xad,0xc8//0xc8,0x7318//0x7f,0x2d6c//0x99,0x8fe7//0xc5,0x13ec//0x55,0x5abe//0xca,0xbb98//0xe8,0x2ee//0xfa,0x304f//0x95,0x6c48//0x6e,0x6270//0xe1,0x820//0x28,0x6b6c//0x6e,0x16b3//0x95,0x2d0//0x90,0x258//0x8,0xd227//0xed,0x39c0//0x58,0x42//0x16,0x237d//0x4f,0x2d0c//0x5d,0x225e//0x35,0xb88//0x12,0x55d3//0xad,0x3840//0xc8,0x1555//0x7f,0x2211//0x99,0x3d9//0xc5,0x8a2//0x55,0xe34//0xca,0x6bd8//0xe8,0xbc7a//0xfa,0x1a31//0x95,0x58f2//0x6e,0x189c//0xe1,0x4d8//0x28,0x46e6//0x6e,0x5edf//0x95,0x8160//0x90,0x208//0x8,0xe1e4//0xed,0x478//0x58,0x119e//0x16,0x1371//0x4f,0//0x5d,0x2d57//0x35,0x534//0x12,0x96b3//0xad,0xabe0//0xc8,0x7495//0x7f,0x5a3f//0x99,0x7ef9//0xc5,0x44bb//0x55,0x610e//0xca,0x828//0xe8,0x445c//0xfa,0x1daf//0x95,0x3de0//0x6e,0x5460//0xe1,0x870//0x28,0x66b2//0x6e,0x2953//0x95,0x7c50//0x90,0x190//0x8,0xb2ad//0xed,0x3b78//0x58,0x1474//0x16,0x1fc9//0x4f,0x3966//0x5d,0x282a//0x35,0xcf0//0x12,0x7a51//0xad,0x7aa8//0xc8,0x24b6//0x7f,0x90a2//0x99,0x25b5//0xc5,0x15ea//0x55,0x8baa//0xca,0x8538//0xe8,0x109a//0xfa,0x4e93//0x95,0x2864//0x6e,0x1c20//0xe1,0x1b08//0x28,0x24f4//0x6e,0x5a37//0x95,0x120//0x90,0x378//0x8,0xbfa3//0xed,0x11e0//0x58,0xede//0x16,0x4a1//0x4f,0x555f//0x5d,0x2b7a//0x35,0x3cc//0x12,0x5d42//0xad,0x3070//0xc8,0x2ca6//0x7f,0x6897//0x99,0x5a09//0xc5,0x4bb4//0x55,0x1f90//0xca,0x3e88//0xe8,0x89b2//0xfa,0x6cd7//0x95,0x686a//0x6e,0x2409//0xe1,0x1798//0x28,0x150e//0x6e,0x8e04//0x95,0x8040//0x90,0x530//0x8,0x29a9//0xed,0x10d8//0x58,0x53e//0x16,0x4395//0x4f,0x1740//0x5d,0x6a//0x35,0x1086//0x12,0x6ccd//0xad,0x6400//0xc8,0x2b29//0x7f,0x3366//0x99,0x93c//0xc5,0x2134//0x55,0xa748//0xca,0x88d8//0xe8,0xa7f8//0xfa,0x3462//0x95,0x2940//0x6e,0x972c//0xe1,0xf00//0x28,0x5b18//0x6e,0x88c7//0x95,0x8e50//0x90,0x630//0x8,0xcbac//0xed,0x5438//0x58,0xe5a//0x16,0x145e//0x4f,0x216c//0x5d,0x3323//0x35,0x3de//0x12,0x74e9//0xad,0x2198//0xc8,0x2339//0x7f,0x8c73//0x99,0x954a//0xc5,0x8a2//0x55,0x13ba//0xca,0x9af8//0xe8,0xd9c6//0xfa,0x6670//0x95,0x55f0//0x6e,0x8bbf//0xe1,0x758//0x28,0x3020//0x6e,0x4f28//0x95,0x4890//0x90,0x560//0x8,0xc26a//0xed,0x4a98//0x58,0x84//0x16,0x1687//0x4f,0xc5a//0x5d,0x30a7//0x35,0//0x12,0x87d5//0xad,0x2fa8//0xc8,0x5f40//0x7f,0x7eb4//0x99,0x9aad//0xc5,0x21de//0x55,0x7e40//0xca,0x5e40//0xe8,0xfa//0xfa,0x838a//0x95,0x6c48//0x6e,0xc6a2//0xe1,0x988//0x28,0x6946//0x6e,0x6133//0x95,0x8dc0//0x90,0x1f8//0x8,0xd7b5//0xed,0x4620//0x58,0x153a//0x16,0x49c1//0x4f,0x4392//0x5d,0x2b10//0x35,0x10f2//0x12,0x85ce//0xad,0xaca8//0xc8,0x60bd//0x7f,0x9306//0x99,0x8d98//0xc5,0x44bb//0x55,0x154e//0xca,0x2358//0xe8,0x2904//0xfa,0x17dd//0x95,0x31d8//0x6e,0x6a59//0xe1,0x25f8//0x28,0x47c2//0x6e,0x84b4//0x95,0x7230//0x90,0x548//0x8,0xc09//0xed,0x4e08//0x58,0x554//0x16,0x22df//0x4f,0x4335//0x5d,0x35//0x35,0x870//0x12,0x17a7//0xad,0x5780//0xc8,0x2fa0//0x7f,0x718e//0x99,0x7747//0xc5,0x1d38//0x55,0xc86c//0xca,0x5700//0xe8,0xe196//0xfa,0x320e//0x95,0xc76//0x6e,0x6270//0xe1,0x1a18//0x28,0x63b0//0x6e,0x7468//0x95,0x90//0x90,0x368//0x8,0x1cb3//0xed,0x4678//0x58,0xf62//0x16,0x2693//0x4f,0x55bc//0x5d,0x1ea4//0x35,0x29a//0x12,0x29e6//0xad,0x1900//0xc8,0x2535//0x7f,0x13b9//0x99,0xaeaf//0xc5,0x18e7//0x55,0x69bc//0xca,0x45c8//0xe8,0x7530//0xfa,0x8549//0x95,0x6c48//0x6e,0x448e//0xe1,0xff0//0x28,0x5816//0x6e,0x33cd//0x95,0x22e0//0x90,0x3b0//0x8,0xbfa3//0xed,0x55f0//0x58,0x4ba//0x16,0x105b//0x4f,0x2853//0x5d,0x9bb//0x35,0xd8//0x12,0x4441//0xad,0xb608//0xc8,0x4d64//0x7f,0x3bc4//0x99,0x5c58//0xc5,0x1342//0x55,0x4fb2//0xca,0x1d0//0xe8,0xc544//0xfa,0x37e//0x95,0x6b6c//0x6e,0xc31e//0xe1,0xd98//0x28,0x5b18//0x6e,0x57e3//0x95,0x64b0//0x90,0x240//0x8,0xd98f//0xed,0x4e60//0x58,0x53e//0x16,0x4a10//0x4f,0x4107//0x5d,0x21f4//0x35,0xc4e//0x12,0x81c0//0xad,0x2008//0xc8,0x1ec2//0x7f,0x1de2//0x99,0x2ca2//0xc5]
starters = [0xfffffffffffa00b1,0xfffffffffffa608a,0xfffffffffffa0a1e,0xfffffffffffa7510,0xfffffffffff9b125,0xfffffffffff9e59c,0xfffffffffff85543,0xfffffffffff99fda,0xfffffffffff967ac,0xfffffffffffa22b9,0xfffffffffffa49e3,0xfffffffffff86f81,0xfffffffffffb7d48,0xfffffffffff8a759,0xfffffffffff88a1d,0xfffffffffff9f131,0xfffffffffffa59be,0xfffffffffff78985,0xfffffffffff9924c,0xfffffffffff70587,0xfffffffffff9ac6e,0xfffffffffff92853,0xfffffffffffa0636,0xfffffffffff8dda8,0xffffffffffff2664,0xfffffffffffeae0c,0xffffffffffff36ed,0xfffffffffffe82d5,0xfffffffffffe6984,0xfffffffffffdf521,0xfffffffffffe7f1e,0xfffffffffffe56e1,0xfffffffffffefff1,0xffffffffffff1002,0xffffffffffff0b7f,0xfffffffffffec4b9,0xfffffffffffe8118,0xfffffffffffeaca5,0xffffffffffff87af,0xffffffffffffa4d9,0xfffffffffffe3e11]
D=0
for i in range(a):
G=starters[i]
for j in range(len(smt)):
G += smt[j] * multiplier[i*len(smt)+j]
G &= 0xffffffffffffffff
G &= 0xffffff
D += G
We have reversed the first 93585 lines.
From here, we see a change in code
mov [0xa29042], 0x0
mov B, 0xa59afa
mov B.st_size, 0x240
mov [0x804aca], [B] (576 bytes)
mov E, 0x0
mov [0x804000], 0x0
mov [0x804000], 0x0
mov [0x804000], 0x0
mov [0x804000], 0x0
mov [0x804000], 0x0
mov [0x804000], 0x0
mov [0xa290c2], 0x5500404040c7c748
mov [0xa290ca], 0xc7e87d8948e58948
mov [0xa290d2], 0x45c700000000fc45
...
We deduce that this must indicate the end of the first half of the flag checker and guess that D==0 as all the starting values were negative numbers.
Thus, we use z3 to first find the values of smt.
def brute():
smt = [BitVec('smt_{}'.format(hex(i)), 7) for i in range(len(smt))]
s = Solver()
D=0
for i in range(a):
G = 0
for j in range(len(smt)):
G += smt[j] * multiplier[i*len(smt)+j]
G &= 0xffffffffffffffff
s.add(G == 0x10000000000000000-starters[i])
print(s.check())
print(s.model())
# smt == [134,72,8,237,30,49,89,229,232,232,228,17,242,81,243,1,225,114,46,224,109,91,103,182]
From here, we can brute force the beginning bytes of the flag
def scramble(flag, idx):
D = 0
mem = list(range(256))
for i in range(256):
D += mem[i]
D += ord(flag[(i&1)+idx])
D %= 256
mem[D],mem[i] = mem[i], mem[D]
D = 0
B = 0
smt = []
for i in range(3):
D += mem[i]
D %= 256
F = mem[i]
mem[i] = mem[D]
G = mem[i]
mem[D] = F
F += G
F %= 256
smt.append(chr(mem[F]))
return smt
def brute_solve():
goal = [134,72,8,237,30,49,89,229,232,232,228,17,242,81,243,1,225,114,46,224,109,91,103,182]
goal = list(map(chr, goal))
flag = ''
for i in range(8):
for j in range(128):
found = False
for k in range(128):
flagg = flag+chr(j)+chr(k)
arr = scramble(flagg, i*2)
if arr == goal[3*i:3*i+3]:
flag = flagg
print(flag)
found = True
break
if found:
break
From here, we have our first flag CTF{H0p3_y0u_l1k
Reversing the Flag Part 2⌗
Ok, we have found the first half of the flag and only have ~7k lines left to reverse. Knowing the first half of the flag, we can put a place holder value of the second half
flag = 'CTF{H0p3_y0u_l1kABCDEFGHIJKL'
mov [0xa29042], 0x0
mov B, 0xa59afa
mov B.st_size, 0x240
mov [0x804aca], [B] (576 bytes)
# Zeros out symbols?
mov E, 0x0
mov [0x804000], 0x0
mov [0x804000], 0x0
mov [0x804000], 0x0
mov [0x804000], 0x0
mov [0x804000], 0x0
mov [0x804000], 0x0
mov [0xa290c2], 0x5500404040c7c748
mov [0xa290ca], 0xc7e87d8948e58948
mov [0xa290d2], 0x45c700000000fc45
mov [0xa290da], 0x8b3beb00000000f8
mov [0xa290e2], 0x458b48d06348fc45
mov [0xa290ea], 0x3c00b60fd00148e8
mov [0xa290f2], 0x6348fc458b147620
mov [0xa290fa], 0xd00148e8458b48d0
mov [0xa29102], 0xb807767e3c00b60f
mov [0xa2910a], 0xb805eb00000001
mov [0xa29112], 0x4583f84509000000
mov [0xa2911a], 0xbf7e1bfc7d8301fc
mov [0xa29122], 0x8b48d06348fc458b
mov [0xa2912a], 0xb60fd00148e845
mov [0xa29132], 0x458bf84509c0b60f
mov [0xa2913a], 0xc3c35d9848f8
# Some sort of data?
mov C, 0xa290c2
mov [0x8040ac], 0x1000a0000001a
# ???
add64 E, C
# E = 0xa290c2?
mov B, 0xa59caa
mov B.st_size, 0x90
mov [0xa290c2], [B] (144 bytes)
# Zeros out data
mov B, &E
mov B.st_size, 0x8
mov [0xa293ba], [B] (8 bytes)
add64 D, D + 0xa290c2
# D += E
Ok, I found add64 E, C to be very confusing as it is later used in # D += E. In the previous section, D was used to keep track of the sum results calculated based off the input.
Time sink #3, not bothering to use a debugger on the original binary to double check my assumptions
Opening up a debugger and setting a hardware watch at add64 D, D + 0xa290c2 with awatch *0xa293ba, we see the value of E is infact not 0xa290c2 but 0.
So what is going on? Well, the most interesting instruction here is mov [0x8040ac], 0x1000a0000001a as it references an address in the symbol table specifically C.st_name.
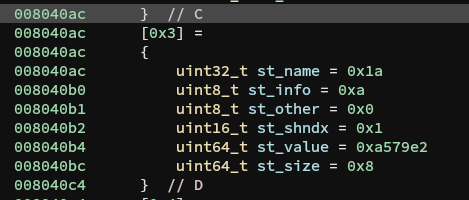
Here, we see mov [0x8040ac], 0x1000a0000001a not only overwrites C.st_name but also C.st_info, C.st_other, and C.st_shndx.
Looking at the source code of the relocation machine, we see
struct link_map *sym_map = RESOLVE_MAP (map, scope, &sym, version,
r_type);
ElfW(Addr) value = SYMBOL_ADDRESS (sym_map, sym, true);
if (sym != NULL
&& __glibc_unlikely (ELFW(ST_TYPE) (sym->st_info) == STT_GNU_IFUNC)
&& __glibc_likely (sym->st_shndx != SHN_UNDEF)
&& __glibc_likely (!skip_ifunc))
{
value = ((ElfW(Addr) (*) (void)) value) ();
}
switch (r_type)
{
case R_X86_64_SIZE64:
/* Set to symbol size plus addend. */
*(Elf64_Addr *) (uintptr_t) reloc_addr
= (Elf64_Addr) sym->st_size + reloc->r_addend;
break;
}
...
Here, we see elf_machine_rela will jump to shellcode at sym.st_value if sym != NULL and sym->st_shndx != SHN_UNDEF and sym->st_info == STT_GNU_IFUNC (SHN_UNDEF = 0, STT_GNU_IFUNC = 0xa). We notice that mov [0x8040ac], 0x1000a0000001a sets C.st_shndx to 1 and C.st_info to 0xa. Thus add64 E, C will jump to shellcode at C and take the return value of the shellcode and add it to E.
Here, we will patch our code to dump the disassembly
def sym(r_offset, r_symbol, r_addend):
if r_symbol not in symbols_lookup:
print("AAAAAA", hex(r_symbol))
exit(0)
if r_addend == 0:
print('add64 {}, {}'.format(parse_addr(r_offset), symbols_lookup[r_symbol]))
else:
print('add64 {}, {} + {}'.format(parse_addr(r_offset), symbols_lookup[r_symbol], hex(r_addend)))
st_info = u8(elf.read(symbols_to_addr[r_symbol]-4, 1))
if st_info == 0xa:
print("JUMPING TO SHELLCODE")
print("#"*20)
sym_val = u64(elf.read(symbols_to_addr[r_symbol], 8))
sc = elf.read(sym_val, 20*8)
dd = disasm(sc).split('\n')
for i in dd:
print(i)
if 'ret' in i:
break
print("{} = RETVAL", parse_addr(r_offset))
print("#"*20)
elf.write(r_offset, p64(0))
else:
sym_val = u64(elf.read(symbols_to_addr[r_symbol], 8))
elf.write(r_offset, p64((r_addend+sym_val)&0xffffffffffffffff))
The new disassembly dump can be found here
mov [0xa290c2], 0x5500404040c7c748
mov [0xa290ca], 0xc7e87d8948e58948
mov [0xa290d2], 0x45c700000000fc45
mov [0xa290da], 0x8b3beb00000000f8
mov [0xa290e2], 0x458b48d06348fc45
mov [0xa290ea], 0x3c00b60fd00148e8
mov [0xa290f2], 0x6348fc458b147620
mov [0xa290fa], 0xd00148e8458b48d0
mov [0xa29102], 0xb807767e3c00b60f
mov [0xa2910a], 0xb805eb00000001
mov [0xa29112], 0x4583f84509000000
mov [0xa2911a], 0xbf7e1bfc7d8301fc
mov [0xa29122], 0x8b48d06348fc458b
mov [0xa2912a], 0xb60fd00148e845
mov [0xa29132], 0x458bf84509c0b60f
mov [0xa2913a], 0xc3c35d9848f8
mov C, 0xa290c2
mov C.st_name, 0x1000a0000001a
add64 E, C
JUMPING TO SHELLCODE
####################
0: 48 c7 c7 40 40 40 00 mov rdi, 0x404040
7: 55 push rbp
8: 48 89 e5 mov rbp, rsp
b: 48 89 7d e8 mov QWORD PTR [rbp-0x18], rdi
f: c7 45 fc 00 00 00 00 mov DWORD PTR [rbp-0x4], 0x0
16: c7 45 f8 00 00 00 00 mov DWORD PTR [rbp-0x8], 0x0
1d: eb 3b jmp 0x5a
1f: 8b 45 fc mov eax, DWORD PTR [rbp-0x4]
22: 48 63 d0 movsxd rdx, eax
25: 48 8b 45 e8 mov rax, QWORD PTR [rbp-0x18]
29: 48 01 d0 add rax, rdx
2c: 0f b6 00 movzx eax, BYTE PTR [rax]
2f: 3c 20 cmp al, 0x20
31: 76 14 jbe 0x47
33: 8b 45 fc mov eax, DWORD PTR [rbp-0x4]
36: 48 63 d0 movsxd rdx, eax
39: 48 8b 45 e8 mov rax, QWORD PTR [rbp-0x18]
3d: 48 01 d0 add rax, rdx
40: 0f b6 00 movzx eax, BYTE PTR [rax]
43: 3c 7e cmp al, 0x7e
45: 76 07 jbe 0x4e
47: b8 01 00 00 00 mov eax, 0x1
4c: eb 05 jmp 0x53
4e: b8 00 00 00 00 mov eax, 0x0
53: 09 45 f8 or DWORD PTR [rbp-0x8], eax
56: 83 45 fc 01 add DWORD PTR [rbp-0x4], 0x1
5a: 83 7d fc 1b cmp DWORD PTR [rbp-0x4], 0x1b
5e: 7e bf jle 0x1f
60: 8b 45 fc mov eax, DWORD PTR [rbp-0x4]
63: 48 63 d0 movsxd rdx, eax
66: 48 8b 45 e8 mov rax, QWORD PTR [rbp-0x18]
6a: 48 01 d0 add rax, rdx
6d: 0f b6 00 movzx eax, BYTE PTR [rax]
70: 0f b6 c0 movzx eax, al
73: 09 45 f8 or DWORD PTR [rbp-0x8], eax
76: 8b 45 f8 mov eax, DWORD PTR [rbp-0x8]
79: 48 98 cdqe
7b: 5d pop rbp
7c: c3 ret
('{} = RETVAL', 'E')
####################
mov B, 0xa59caa
mov B.st_size, 0x90
mov [0xa290c2], [B] (144 bytes)
mov B, &E
mov B.st_size, 0x8
mov [0xa293ba], [B] (8 bytes)
add64 D, D
Quickly shoving the shellcode into binja, we see
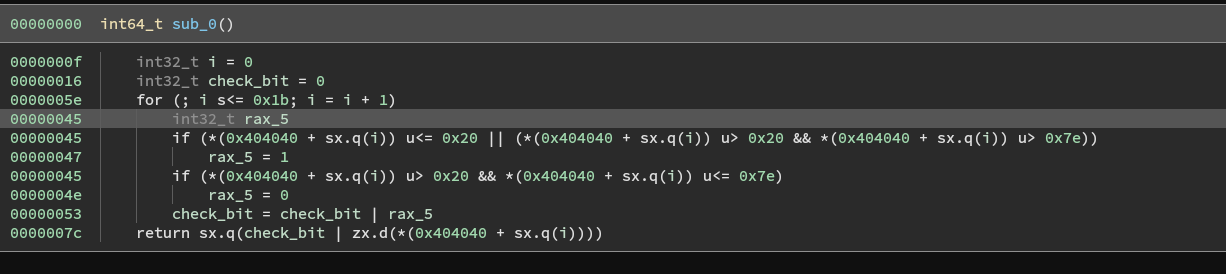
The shellcode checks the first 27 bytes of the flag and makes sure each character satifies 0x20 < char < 0x7e.
Looking at the following shellcode, we see
add64 D, D
mov [0xa293ba], 0x0
mov E, 0x0
mov G, 0xffffffffffff2664
# G = 0xffffffffffff2664
mov B, 0x404050
mov B.st_size, 0x1
mov E, [B] (1 bytes)
# E = serial[0x10]
mov F, 0x0
mov B, &F
mov B.st_size, 0x8
mov [0xa294c2], [B] (8 bytes)
add64 F, F
mov [0xa294c2], 0x0
mov B, &E
mov [0xa29522], [B] (8 bytes)
add64 F, F + 0x51
mov [0xa29522], 0x0
mov B, &F
mov [0xa29582], [B] (8 bytes)
add64 F, F + 0x51
mov [0xa29582], 0x0
mov [0xa295ca], [B] (8 bytes)
add64 F, F + 0xa2
mov [0xa295ca], 0x0
mov [0xa29612], [B] (8 bytes)
add64 F, F + 0x144
mov [0xa29612], 0x0
mov B, &E
mov [0xa29672], [B] (8 bytes)
add64 F, F + 0x51
mov [0xa29672], 0x0
mov B, &F
mov [0xa296d2], [B] (8 bytes)
add64 F, F + 0x2d9
mov [0xa296d2], 0x0
mov B, &E
mov [0xa29732], [B] (8 bytes)
add64 F, F + 0x51
mov [0xa29732], 0x0
mov B, &F
mov [0xa29792], [B] (8 bytes)
add64 F, F + 0x603
mov [0xa29792], 0x0
mov [0xa297da], [B] (8 bytes)
add64 F, F + 0xc06
mov [0xa297da], 0x0
mov [0xa29822], [B] (8 bytes)
add64 G, G + 0x180c
# G += serial[0x10]*76
mov [0xa29822], 0x0
mov B, 0x404051
Ok, this is quite similar code to the first flag checker. But looking at few lines further, we see
mov [0xa29c5a], 0x0
mov B, 0x404052
mov B.st_size, 0x1
mov E, [B] (1 bytes)
# E = serial[0x12]
mov [0x804000], 0x0
mov [0xa29cc2], 0x9f008040e4252480
mov [0xa29cca], 0xc3
mov C, 0xa29cc2
mov C.st_name, 0x1000a0000001a
add64 [0xa29cc2], C
JUMPING TO SHELLCODE
####################
0: 80 24 25 e4 40 80 00 9f and BYTE PTR ds:0x8040e4, 0x9f
# E &= 0x9f
8: c3 ret
('{} = RETVAL', '[0xa29cc2]')
####################
mov B, 0xa59d22
mov B.st_size, 0x18
mov [0xa29cc2], [B] (24 bytes)
mov B, &E
mov B.st_size, 0x8
mov [0xa29df2], [B] (8 bytes)
add64 G, G + 0x53
# G += E
Taking a look at some other pieces of shellcode, we see all the instructions are all of the form of op E, val; ret; where the operation can be and, or, xor, shl, shr, rol, or ror.
After looking at the pattern, we see this second half checks the rest of the flag and repeats 17 times. Using more sublime magic, we can extract the constants and shellcode.
def _and(val):
return lambda x: x&val
def _or(val):
return lambda x: x|val
def _xor(val):
return lambda x: x^val
def _shl(val):
val%=8
return lambda x: (x << val) & 0xff
def _shr(val):
val %= 8
# print(val)
return lambda x: LShR(x,val) & 0xff
# return lambda x: (x >> val) & 0xff
def _rol(val):
rol = lambda vall, r_bits: ((_shl(r_bits)(vall)) | (_shr(8 - r_bits)(vall))) & 0xff
return lambda x: rol(x, val)
def _ror(val):
ror = lambda vall, r_bits: ((_shl(8 - r_bits)(vall)) | (_shr(r_bits)(vall))) & 0xff
return lambda x: ror(x, val)
multiplier = [0x134c//0x41,0x1ad0//0x42,0x43//0x43,0x44//0x44,0x45//0x45,0x46//0x46,0x174c//0x47,0xd8//0x48,0x49//0x49,0x4a//0x4a,0x8ca//0x4b,0x452c//0x4c,0x1185//0x41,0x25a4//0x42,0x20b7//0x43,0x44//0x44,0x3405//0x45,0x3d86//0x46,0x18f6//0x47,0x21c0//0x48,0x49//0x49,0x43ee//0x4a,0x4b//0x4b,0x4c//0x4c,0x138d//0x41,0x42//0x42,0x40a5//0x43,0x2ec0//0x44,0x17fd//0x45,0x196e//0x46,0x47//0x47,0x1128//0x48,0x6d8//0x49,0x4a//0x4a,0x4b//0x4b,0x4c//0x4c,0x2512//0x41,0x42//0x42,0x13a1//0x43,0x2d28//0x44,0x45//0x45,0x2c4c//0x46,0x3f3c//0x47,0x678//0x48,0x49//0x49,0x4154//0x4a,0x3c0f//0x4b,0x4c//0x4c,0x41//0x41,0x25e6//0x42,0x1a6f//0x43,0x34dc//0x44,0x3084//0x45,0x1856//0x46,0x47//0x47,0x948//0x48,0x28c7//0x49,0x151a//0x4a,0x4281//0x4b,0xe8c//0x4c,0x285f//0x41,0x3f2a//0x42,0x1ee2//0x43,0x39a4//0x44,0x8e5//0x45,0x2aee//0x46,0x47//0x47,0x2d0//0x48,0x2281//0x49,0x349c//0x4a,0x22dd//0x4b,0x44e0//0x4c,0x3b29//0x41,0x42//0x42,0x131b//0x43,0x44//0x44,0x1254//0x45,0x2aa8//0x46,0x3117//0x47,0x48//0x48,0x49//0x49,0x33be//0x4a,0x168f//0x4b,0x40b8//0x4c,0x41//0x41,0x42//0x42,0xd16//0x43,0xc38//0x44,0x303f//0x45,0x44a2//0x46,0x1179//0x47,0x1320//0x48,0x1df1//0x49,0x4a//0x4a,0x4731//0x4b,0x3194//0x4c,0x2cf1//0x41,0x42//0x42,0x1f25//0x43,0x44//0x44,0xb52//0x45,0x13f6//0x46,0x11c//0x47,0x48//0x48,0x2a34//0x49,0x4a//0x4a,0x4b//0x4b,0x3a30//0x4c,0x41//0x41,0x40f8//0x42,0xf2e//0x43,0x3894//0x44,0x78c//0x45,0x46//0x46,0x47//0x47,0x48//0x48,0x49//0x49,0x11a2//0x4a,0xf3c//0x4b,0x11d0//0x4c,0x2922//0x41,0x42//0x42,0x10c//0x43,0x44//0x44,0x37cb//0x45,0x2300//0x46,0x47//0x47,0x48//0x48,0x68f//0x49,0x4a//0x4a,0x485d//0x4b,0x4c//0x4c,0xfbe//0x41,0x42//0x42,0x57f//0x43,0x3f7c//0x44,0x2715//0x45,0x1c2a//0x46,0x47//0x47,0x48//0x48,0x3478//0x49,0x45aa//0x4a,0x1518//0x4b,0x4c//0x4c,0x41//0x41,0x42//0x42,0x1a6f//0x43,0x3278//0x44,0x10fb//0x45,0x3b56//0x46,0x3b5a//0x47,0x2568//0x48,0x49//0x49,0x4a//0x4a,0xe1//0x4b,0x35bc//0x4c,0x334a//0x41,0x30ba//0x42,0xff7//0x43,0x2b08//0x44,0x3672//0x45,0x46//0x46,0x35ce//0x47,0x48//0x48,0x49//0x49,0x2c3a//0x4a,0x4b//0x4b,0x4c//0x4c,0x3cf//0x41,0xa92//0x42,0x43//0x43,0x44//0x44,0x45//0x45,0x2daa//0x46,0x47//0x47,0x48//0x48,0xa44//0x49,0x2266//0x4a,0x4b//0x4b,0x4c//0x4c,0x41//0x41,0x42//0x42,0x43//0x43,0x44//0x44,0x45//0x45,0x46//0x46,0x47//0x47,0x48//0x48,0x49//0x49,0x47b0//0x4a,0x4b//0x4b,0x18f0//0x4c,0x10c2//0x41,0x28bc//0x42,0x27c8//0x43,0xd48//0x44,0x1773//0x45,0x33f4//0x46,0x46b9//0x47,0x15a8//0x48,0x49//0x49,0x32e//0x4a,0x4b//0x4b,0x43fc//0x4c]
multiplier = [multiplier[i:i+12] for i in range(0, len(multiplier), 12)]
# 0xa293f2: mov G, 0xffffffffffff2664
multiplier[0][0x2] = _and(0x9f)
multiplier[0][0x3] = _rol(0x56)
multiplier[0][0x4] = _or(0x47)
multiplier[0][0x5] = _shr(0x0)
multiplier[0][0x8] = _shl(0x2)
multiplier[0][0x9] = _or(0xb8)
# 0xa2b6ea: mov G, 0xfffffffffffeae0c
multiplier[1][0x3] = _and(0xfc)
multiplier[1][0x8] = _xor(0x6e)
multiplier[1][0xa] = _ror(0xa)
multiplier[1][0xb] = _shr(0x6)
# 0xa2e53a: mov G, 0xffffffffffff36ed
multiplier[2][0x1] = _rol(0x4)
multiplier[2][0x6] = _shl(0x1)
multiplier[2][0x9] = _and(0x3a)
multiplier[2][0xa] = _rol(0xed)
multiplier[2][0xb] = _xor(0x8a)
# 0xa30f82: mov G, 0xfffffffffffe82d5
multiplier[3][0x1] = _shl(0x3)
multiplier[3][0x4] = _and(0xca)
multiplier[3][0x8] = _and(0x38)
multiplier[3][0xb] = _ror(0xe5)
# 0xa33ce2: mov G, 0xfffffffffffe6984
multiplier[4][0x0] = _and(0xfc)
multiplier[4][0x6] = _xor(0xc)
# 0xa3702a: mov G, 0xfffffffffffdf521
multiplier[5][0x6] = _shr(0x1)
# 0xa3aa02: mov G, 0xfffffffffffe7f1e
multiplier[6][0x1] = _or(0x31)
multiplier[6][0x3] = _xor(0x63)
multiplier[6][0x7] = _and(0x9a)
multiplier[6][0x8] = _ror(0x7a)
# 0xa3d822: mov G, 0xfffffffffffe56e1
multiplier[7][0x0] = _xor(0x7)
multiplier[7][0x1] = _shl(0x6)
multiplier[7][0x9] = _shl(0x4)
# 0xa40b0a: mov G, 0xfffffffffffefff1
multiplier[8][0x1] = _xor(0xe7)
multiplier[8][0x3] = _and(0xae)
multiplier[8][0x7] = _ror(0x2f)
multiplier[8][0x9] = _and(0xd)
multiplier[8][0xa] = _and(0x6b)
# 0xa431c2: mov G, 0xffffffffffff1002
multiplier[9][0x5] = _rol(0xfb)
multiplier[9][0x6] = _xor(0xfa)
multiplier[9][0x7] = _ror(0xf4)
multiplier[9][0x8] = _ror(0xdb)
# 0xa45b32: mov G, 0xffffffffffff0b7f
multiplier[10][0x1] = _ror(0x3b)
multiplier[10][0x3] = _shl(0x0)
multiplier[10][0x6] = _ror(0x15)
multiplier[10][0x7] = _or(0x48)
multiplier[10][0x9] = _rol(0x1)
multiplier[10][0xb] = _shr(0x3)
# 0xa4803a: mov G, 0xfffffffffffec4b9
multiplier[11][0x1] = _or(0x8b)
multiplier[11][0x6] = _shr(0x0)
multiplier[11][0x7] = _rol(0xe4)
multiplier[11][0xb] = _xor(0x26)
# 0xa4ae2a: mov G, 0xfffffffffffe8118
multiplier[12][0x0] = _and(0xad)
multiplier[12][0x1] = _xor(0x17)
multiplier[12][0x8] = _xor(0x73)
multiplier[12][0x9] = _or(0x66)
# 0xa4dc7a: mov G, 0xfffffffffffeaca5
multiplier[13][0x5] = _shl(0x0)
multiplier[13][0x7] = _ror(0x14)
multiplier[13][0x8] = _shl(0x3)
multiplier[13][0xa] = _and(0xd0)
multiplier[13][0xb] = _xor(0xff)
# 0xa507fa: mov G, 0xffffffffffff87af
multiplier[14][0x2] = _rol(0xb4)
multiplier[14][0x3] = _shr(0x3)
multiplier[14][0x4] = _ror(0x64)
multiplier[14][0x6] = _rol(0x51)
multiplier[14][0x7] = _rol(0x20)
multiplier[14][0xa] = _xor(0xd5)
multiplier[14][0xb] = _shl(0x0)
# 0xa52a4a: mov G, 0xffffffffffffa4d9
multiplier[15][0x0] = _and(0xdf)
multiplier[15][0x1] = _shr(0x5)
multiplier[15][0x2] = _and(0x16)
multiplier[15][0x3] = _and(0x8c)
multiplier[15][0x4] = _or(0x42)
multiplier[15][0x5] = _and(0x51)
multiplier[15][0x6] = _or(0xae)
multiplier[15][0x7] = _shr(0x3)
multiplier[15][0x8] = _xor(0x8e)
multiplier[15][0xa] = _and(0x93)
# 0xa544ba: mov G, 0xfffffffffffe3e11
multiplier[16][0x8] = _xor(0xff)
multiplier[16][0xa] = _and(0x94)
starters = [0xffffffffffff2664,0xfffffffffffeae0c,0xffffffffffff36ed,0xfffffffffffe82d5,0xfffffffffffe6984,0xfffffffffffdf521,0xfffffffffffe7f1e,0xfffffffffffe56e1,0xfffffffffffefff1,0xffffffffffff1002,0xffffffffffff0b7f,0xfffffffffffec4b9,0xfffffffffffe8118,0xfffffffffffeaca5,0xffffffffffff87af,0xffffffffffffa4d9,0xfffffffffffe3e11]
for idx in range(a):
G = starters[idx]
for i in range(0xc):
if isinstance(multiplier[idx][i], int):
G += flag[i+0x10] * multiplier[idx][i]
else:
G += multiplier[idx][i](flag[i+0x10])
# print(hex(G))
G &= 0xffffffffffffffff
G &= 0xffffff
D += G
Ok! We have everything we need to calculate the second half of the flag. We can use z3 again.
flag = [BitVec('flag_{}'.format(hex(i)), 64) for i in range(0xc)]
s = Solver()
for i in flag:
s.add(0x20 < i)
s.add(i < 0x7e)
for idx in range(a):
G = starters[idx]
for i in range(0xc):
if isinstance(multiplier[idx][i], int):
G += flag[i] * multiplier[idx][i]
else:
G += multiplier[idx][i](flag[i])
# print(hex(G))
G &= 0xffffffffffffffff
G &= 0xffffff
s.add(G == 0)
D += G
print(s.check())
print(s.model())
Our second half of the flag! 3_3LF_m4g1c}
Flag: CTF{H0p3_y0u_l1k3_3LF_m4g1c}
Post-mordem⌗
This is my second time participating in GoogleCTF and my first time solving a challenge. Before the competition began, I set myself the goal of solving a hard challenge to show myself how much I have progressed. >24 hours later and getting stuck several times, Having solve the eldar is such a great personal achievement for myself.
This is certainly a very original challenge and I like to thank the author for a great challenge!